Introduction
Keras, a preferred deep-learning library, has made it easier than ever to construct and practice such fashions. One essential side of the coaching course of is choosing the fitting loss operate to optimize your mannequin’s efficiency.
However first, let’s perceive what a loss operate is.
Within the realm of deep studying, a loss operate measures the distinction between the mannequin’s predictions and the bottom fact. It’s the driving pressure behind the coaching course of, because it gives the gradients needed to regulate the mannequin’s weights by way of backpropagation. Throughout every iteration, the loss is computed, and the mannequin’s weights are up to date to attenuate this worth. This course of continues till no vital enhancements within the analysis metric are noticed.
Whereas the analysis metric (e.g., F1 rating or AUC) stays constant all through your machine studying mission, the loss operate may be fine-tuned and tailored to realize one of the best efficiency doable. In essence, the loss operate is as essential to the success of your mannequin because the architecture and the optimizer. Due to this fact, it’s necessary to fastidiously think about your choices when selecting the best loss operate in your downside.
A current examine explored the impacts of assorted loss capabilities on ultrasound picture high quality utilizing machine studying algorithms, highlighting the significance of selecting the best loss operate for particular purposes (see “Impacts of Losses Functions on the Quality of the Ultrasound Image by Using Machine Learning Algorithms” in IEEE Xplore).
On this article, we’ll delve into numerous loss capabilities provided by Keras and talk about their purposes, enabling you to make an knowledgeable choice when choosing the perfect loss operate in your deep studying mannequin.
Loss capabilities fundamentals
In machine studying, our main goal is to be taught a operate ‘f’ that maps an enter house ‘Φ’ to a desired output house ‘Y’:
f : Φ → Y
To approximate this operate, we use a mannequin ‘fΘ’ parameterized by the parameters ‘Θ’. Given a set of inputs {x0, …, xN} in Φ, we practice the mannequin with corresponding goal variables {y0, …, yN} in Y. In some circumstances, corresponding to with autoencoders, Y is the same as Φ.
A loss operate, denoted as L, quantifies the distinction between the mannequin’s predictions f(xi) and the precise goal values yi by mapping them to an actual quantity l in R. To compute the general loss, we mixture the loss throughout all information factors:
L(f|{x0, …, xN}, {y0, …, yN}) = (1/N) * Σ[N, i=1] L(f(xi), yi) (1)
The optimization downside can then be expressed as:
min f L(f|{x0, …, xN}, {y0, …, yN}) (2)
Within the context of our Keras loss operate article, we goal to discover numerous loss capabilities that can be utilized to quantify the distinction between predicted and precise values, finally serving to us optimize our deep studying fashions.
https://chart-studio.plotly.com/~aayushmittalaayush/14/#/
Which loss capabilities can be found in Keras?
Loss capabilities play a vital function within the success of a deep studying structure. They function the guiding pressure behind the again propagation algorithm, which updates the mannequin’s weights. For that reason, it’s important to decide on loss capabilities which are differentiable. Broadly talking, these capabilities may be categorized into 5 classes: class-wise, pairwise, triplet, quadruplet, and hybrid.
Class-wise loss capabilities examine the output of deep studying fashions with class labels. Some frequent examples embrace Binary Cross Entropy, Categorical Cross Entropy, Imply Squared Error, and LogSoftmax loss. These capabilities can be utilized for regression or classification duties, relying on the issue at hand.
Pairwise loss capabilities, then again, assess the interactions between enter pairs, specializing in each unfavorable and optimistic influences. Some well-liked pairwise loss capabilities embrace Cosine Similarity, Hinge, and Siamese loss.
Triplet and quadruplet loss capabilities think about each unfavorable and optimistic interactions of their formulation. Triplet loss capabilities are based mostly on the unique triplet community loss operate, and most variations are simply mathematical reformulations. Quadruplet loss capabilities, in the meantime, are usually derived from triplet loss capabilities.
Lastly, hybrid loss capabilities are a mix of the opposite kinds of loss capabilities. These capabilities could also be used when a single loss operate doesn’t present passable outcomes.
Binary Cross Entropy
Binary Cross-Entropy is a widely-used loss operate for binary classification issues, the place the goal label is both 0 or 1. It calculates the cross-entropy loss between the true labels and the expected labels. The operate requires two essential inputs:
y_true (true label): The precise label, which is both 0 or 1.
y_pred (predicted worth): The mannequin’s prediction, which is a single floating-point worth that both represents a logit (worth in [-inf, inf] when from_logits=True) or a chance (worth in [0., 1.] when from_logits=False).
Advisable Implementation: (set from_logits=True)
When utilizing the tf.keras API, compile the mannequin as follows:
mannequin.compile(
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
...
)As a standalone operate, think about the next distinctive examples to reveal the utilization of Binary Cross-Entropy:
y_true = [1, 0, 1, 1]
y_pred = [-5.4, 8.7, -1.2, -4.6]
bce = tf.keras.losses.BinaryCrossentropy(from_logits=True)
bce(y_true, y_pred).numpy()Furthermore, Binary Cross-Entropy helps the ‘sample_weight’ attribute and numerous discount varieties, corresponding to ‘sum’ and ‘none’.
Multiclass classification
Categorical Crossentropy
Categorical Cross-Entropy is a widely-used loss operate for multi-class classification issues. It’s used when there are two or extra label courses, and labels are offered in one-hot illustration. For integer labels, use SparseCategoricalCrossentropy loss as a substitute.
Categorical Cross-Entropy Plot Clarification
Implementing Categorical Cross-Entropy
Use the tf.keras.losses.CategoricalCrossentropy class to work with CCE in Keras. The operate takes a number of parameters, together with:
from_logits: A boolean worth specifying whether or not to interpret y_pred as logits or chances.
label_smoothing: A float worth in [0, 1] for label smoothing.
discount: The kind of tf.keras.losses.Discount to use to the loss.
Examples of Implementing CCE
To implement Categorical Cross-Entropy in Keras, you’ll be able to both use the compile() API or as a standalone operate.
Utilizing the compile() API:
mannequin.compile(optimizer=’sgd’, loss=tf.keras.losses.CategoricalCrossentropy())
As a standalone operate:
y_true = [[0, 1, 0], [0, 0, 1]]
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
cce = tf.keras.losses.CategoricalCrossentropy()
cce(y_true, y_pred).numpy()The Poison Loss
Poisson loss is a loss operate typically utilized in count-based regression issues. It computes the distinction between the true depend values and the expected depend values, making it appropriate for duties the place the goal variable represents the variety of occasions occurring in a set interval of time or house.
Implementing Poisson Loss
To work with Poisson loss in Keras, use the tf.keras.losses.Poisson class. This operate accepts the next parameters:
discount: The kind of tf.keras.losses.Discount to use to the loss. The default worth is AUTO.
title: An non-obligatory title for the occasion. Defaults to ‘poisson’.
Examples of Implementing Poisson Loss
You may implement Poisson loss in Keras utilizing the compile() API or as a standalone operate.
Utilizing the compile() API:
mannequin.compile(optimizer='sgd', loss=tf.keras.losses.Poisson())As a standalone operate:
y_true = [[0., 1.], [0., 0.]]
y_pred = [[1., 1.], [0., 0.]]
# Utilizing 'auto'/'sum_over_batch_size' discount sort.
p = tf.keras.losses.Poisson()
p(y_true, y_pred).numpy()
# Calling with 'sample_weight'.
p(y_true, y_pred, sample_weight=[0.8, 0.2]).numpy()
# Utilizing 'sum' discount sort.
p = tf.keras.losses.Poisson(
discount=tf.keras.losses.Discount.SUM)
p(y_true, y_pred).numpy()Within the examples above, the Poisson loss is computed utilizing completely different discount varieties, demonstrating how one can customise the conduct of the loss operate to fit your particular wants.
Kullback-Leibler Divergence Loss
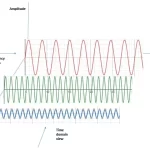
Kullback-Leibler Divergence is a measure of how one chance distribution differs from a second, reference chance distribution. It’s generally utilized in machine studying to measure the distinction between two chance distributions, usually in duties corresponding to unsupervised studying, anomaly detection, and knowledge idea.
This visible illustration demonstrates Kullback-Leibler (KL) divergence
Implementing Kullback-Leibler Divergence Loss
Use the tf.keras.losses.KLDivergence class to work with KL Divergence Loss in Keras. The operate takes a number of parameters, together with:
discount: The kind of tf.keras.losses.Discount to use to the loss.
title: The title for the operation (default is ‘kl_divergence’).
Examples of Implementing Kullback-Leibler Divergence Loss
To implement KL Divergence Loss in Keras, you’ll be able to both use the compile() API or as a standalone operate.
Utilizing the compile() API:
mannequin.compile(optimizer='sgd', loss=tf.keras.losses.KLDivergence())As a standalone operate:
y_true = [[0, 1], [0, 0]]
y_pred = [[0.6, 0.4], [0.4, 0.6]]
kl = tf.keras.losses.KLDivergence()
kl(y_true, y_pred).numpy()Imply Absolute Error
Imply Absolute Error (MAE) is a loss operate that computes the imply of absolutely the distinction between labels (y_true) and predictions (y_pred). It’s used for regression duties, because it measures the common magnitude of errors between predicted and precise values, no matter their path. MAE is much less delicate to outliers in comparison with Imply Squared Error (MSE) and is a typical metric for evaluating the efficiency of regression fashions.
Implementing Imply Absolute Error
Use the tf.keras.losses.MeanAbsoluteError class to work with Imply Absolute Error in Keras. The operate takes a number of parameters, together with:
discount: The kind of tf.keras.losses.Discount to use to the loss.
title: The title for the operation (default is ‘mean_absolute_error’).
Examples of Implementing Imply Absolute Error
To implement Imply Absolute Error in Keras, you’ll be able to both use the compile() API or as a standalone operate.
Utilizing the compile() API:
mannequin.compile(optimizer='sgd', loss=tf.keras.losses.MeanAbsoluteError())As a standalone operate:
y_true = [[0., 1.], [0., 0.]]
y_pred = [[1., 1.], [1., 0.]]
mae = tf.keras.losses.MeanAbsoluteError()
mae(y_true, y_pred).numpy()Cosine Similarity Loss
Cosine Similarity is a measure of similarity between two non-zero vectors of an inside product house, which is extensively utilized in info retrieval and natural language processing. It measures the cosine of the angle between two vectors, leading to a worth between -1 and 1. A worth of -1 signifies a excessive diploma of similarity, 1 signifies a excessive diploma of dissimilarity, and 0 signifies orthogonality.
Implementing Cosine Similarity
Use the tf.keras.losses.CosineSimilarity class to work with Cosine Similarity in Keras. The operate takes a number of parameters, together with:
axis: The axis alongside which the cosine similarity is computed (default is -1).
discount: The kind of tf.keras.losses.Discount to use to the loss.
title: The title for the operation (default is ‘cosine_similarity’).
Examples of Implementing Cosine Similarity
To implement Cosine Similarity in Keras, you’ll be able to both use the compile() API or as a standalone operate.
Utilizing the compile() API:
mannequin.compile(optimizer='sgd', loss=tf.keras.losses.CosineSimilarity(axis=1))As a standalone operate:
y_true = [[0., 1.], [1., 1.]]
y_pred = [[1., 0.], [1., 1.]]
cosine_loss = tf.keras.losses.CosineSimilarity(axis=1)
cosine_loss(y_true, y_pred).NumPy()LogCosh Loss
Log-Cosh Loss is a loss operate that computes the logarithm of the hyperbolic cosine of the prediction error (y_pred – y_true). It’s used as a clean approximation to the Imply Absolute Error (MAE), which makes it much less delicate to outliers within the information. This makes it appropriate to be used in regression duties the place there could also be outliers or noisy information.
Implementing Log-Cosh Loss
Use the tf.keras.losses.LogCosh class to work with Log-Cosh Loss in Keras. The operate takes a number of parameters, together with:
discount: The kind of tf.keras.losses.Discount to use to the loss.
title: The title for the operation (default is ‘log_cosh’).
Examples of Implementing Log-Cosh Loss
To implement Log-Cosh Loss in Keras, you’ll be able to both use the compile() API or as a standalone operate.
Utilizing the compile() API:
mannequin.compile(optimizer='sgd', loss=tf.keras.losses.LogCosh())As a standalone operate:
y_true = [[0., 1.], [0., 0.]]
y_pred = [[1., 1.], [0., 0.]]
l = tf.keras.losses.LogCosh()
l(y_true, y_pred).numpy()Huber loss
Huber Loss is a loss operate generally utilized in regression issues which are much less delicate to outliers in comparison with Imply Squared Error (MSE). The Huber Loss operate is quadratic for small errors and linear for big errors, making it extra sturdy to outliers. This operate has a parameter delta, which determines the purpose at which the loss operate transitions from quadratic to linear. Huber Loss is extensively utilized in sturdy regression and reinforcement studying.
Implementing Huber Loss
Use the tf.keras.losses.Huber class to work with Huber Loss in Keras. The operate takes a number of parameters, together with:
Delta: A float representing the purpose the place the Huber loss operate transitions from quadratic to linear.
Discount: The kind of tf.keras.losses.Discount to use to the loss.
Identify: The title for the operation (default is ‘huber_loss’).
Examples of Implementing Huber Loss
To implement Huber Loss in Keras, you’ll be able to both use the compile() API or as a standalone operate.
Utilizing the compile() API:
mannequin.compile(optimizer='sgd', loss=tf.keras.losses.Huber())As a standalone operate:
y_true = [[0, 1], [0, 0]]
y_pred = [[0.6, 0.4], [0.4, 0.6]]
h = tf.keras.losses.Huber()
h(y_true, y_pred).numpy()Studying Embeddings
Embeddings are a strong approach utilized in machine studying to characterize categorical variables as steady vectors. They permit fashions to seize and be taught relationships between categorical variables in a extra expressive and significant method. Keras gives a easy strategy to create and work with embeddings by way of the Embedding layer.
Right here’s an instance of methods to use the Keras Embedding layer:
from tensorflow.keras.layers import Embedding
embedding_layer = Embedding(input_dim=1000, output_dim=64, input_length=10)On this instance, the input_dim parameter represents the variety of distinctive classes within the enter information (1000 on this case), output_dim is the scale of the embedding vector (64), and input_length is the size of the enter sequence (10).
Now that we’ve mentioned embeddings, let’s dive into some loss capabilities which are appropriate for studying embeddings. These loss capabilities may be significantly helpful when working with complicated information, corresponding to pictures, textual content, or graphs.
Triplet Loss
Triplet loss is a well-liked loss operate used to be taught embeddings in duties like face recognition, the place the objective is to attenuate the gap between an anchor and a optimistic instance whereas maximizing the gap between the anchor and a unfavorable instance. The thought is to be taught a operate that may discriminate between optimistic and unfavorable pairs successfully.
Right here’s a easy instance of methods to implement triplet loss in Keras:
import tensorflow as tf
def triplet_loss(y_true, y_pred, alpha=0.2):
anchor, optimistic, unfavorable = tf.cut up(y_pred, num_or_size_splits=3, axis=1)
positive_distance = tf.reduce_sum(tf.sq.(anchor - optimistic), axis=1)
negative_distance = tf.reduce_sum(tf.sq.(anchor - unfavorable), axis=1)
loss = tf.most(positive_distance - negative_distance + alpha, 0.0)
return tf.reduce_mean(loss)
mannequin.compile(optimizer='adam', loss=triplet_loss)On this instance, the triplet_loss operate takes the expected embeddings for anchor, optimistic, and unfavorable examples and computes the distances between them. The alpha parameter represents a margin that encourages the mannequin to create a separation between optimistic and unfavorable pairs.
Quadruplet loss is an extension of triplet loss and is just like implementing triplet loss. It considers 4 embeddings: anchor, optimistic, unfavorable, and one other unfavorable instance from a distinct class than the anchor. The thought is to be taught a operate that may discriminate between optimistic and unfavorable pairs extra successfully by contemplating extra info.
Creating customized loss capabilities in Keras
In sure conditions, the built-in loss capabilities offered by Keras might not be appropriate in your particular downside. In such circumstances, you’ll be able to create a customized loss operate tailor-made to your wants. On this part, we’ll reveal methods to create a customized loss operate with a singular instance that’s each informative and relevant to real-world situations.
Instance: Customized Loss Perform for Balancing Precision and Recall
Suppose you might be engaged on a binary classification downside the place each false positives and false negatives carry vital prices. On this case, you may wish to steadiness precision (the power to accurately determine optimistic circumstances) and recall (the power to determine all of the precise optimistic circumstances) in your mannequin.
To attain this, you’ll be able to create a customized F-beta loss operate. The F-beta rating is a metric that mixes precision and recall utilizing a parameter beta, which lets you assign completely different weights to precision and recall. The next beta worth prioritizes recall, whereas a decrease beta worth emphasizes precision.
Right here’s how one can outline the customized F-beta loss operate:
import keras.backend as Okay
def custom_fbeta_loss(y_true, y_pred, beta=1):
# Calculate true positives, false positives, and false negatives
true_positives = Okay.sum(y_true * y_pred)
false_positives = Okay.sum((1 - y_true) * y_pred)
false_negatives = Okay.sum(y_true * (1 - y_pred))
# Calculate precision and recall
precision = true_positives / (true_positives + false_positives + Okay.epsilon())
recall = true_positives / (true_positives + false_negatives + Okay.epsilon())
# Calculate the F-beta rating and return its unfavorable worth as a loss
fbeta_score = (1 + beta**2) * (precision * recall) / ((beta**2 * precision) + recall + Okay.epsilon())
return 1 - fbeta_scoreOn this instance, the parameter beta may be adjusted based mostly on the precise necessities of your downside. The default worth of beta is 1, which results in the F1 rating, a generally used metric that balances precision and recall.
After getting outlined the customized loss operate, you need to use it in your mannequin by passing it to the compile() technique:
mannequin.compile(loss=lambda y_true, y_pred: custom_fbeta_loss(y_true, y_pred, beta=1),
optimizer='adam')On this distinctive instance, we’ve demonstrated methods to create a customized loss operate that balances precision and recall for binary classification issues. By following these pointers and adapting the instance above, you’ll be able to create customized loss capabilities that cater to the precise wants of your machine studying tasks, offering each detailed and correct content material.
The add_loss() API
Dealing with Non-Commonplace Losses and Metrics with add_loss() Perform in Keras
Usually, losses and metrics may be computed utilizing the true and predicted values (y_true and y_pred). Nonetheless, there are conditions the place you may require a distinct method. On this part, we’ll discover methods to deal with non-standard losses and metrics utilizing Keras add_loss() operate.
Contemplate a state of affairs the place we wish to add a customized layer to our mannequin that penalizes the activation of a particular layer based mostly on the L1 norm of its weights. This will help in encouraging sparse representations in our mannequin.
Creating the L1 Penalty Layer
To create a customized layer with L1 penalty on weights, we’ll implement the next class:
import tensorflow as tf
from tensorflow.keras import layers
class L1PenaltyLayer(layers.Layer):
def __init__(self, issue, **kwargs):
tremendous(L1PenaltyLayer, self).__init__(**kwargs)
self.issue = issue
def name(self, inputs):
l1_penalty = self.issue * tf.reduce_sum(tf.abs(inputs))
self.add_loss(l1_penalty)
return inputsThis practice layer calculates the L1 penalty on its enter and provides the penalty as a loss utilizing self.add_loss().
With the L1 penalty layer, the mannequin will now encourage sparse representations within the first dense layer whereas coaching. The general loss displayed throughout coaching will embrace each the sparse categorical cross-entropy loss and the L1 penalty loss.
Conclusion
In wrapping up, selecting the best loss operate is important to the success of your deep studying fashions. We’ve mentioned numerous Keras loss capabilities, together with Binary Cross Entropy, Poisson Loss, Kullback-Leibler Divergence Loss, and lots of others, together with sensible examples that can assist you with their implementation.
Bear in mind, the secret is to understand the variations between these loss capabilities and match them to your particular use circumstances. By doing so, you can also make well-informed selections and enhance your mannequin’s efficiency.
References
Lin, Tsung-Yi, et al. “Focal Loss for Dense Object Detection.” 2017 IEEE Worldwide Convention on Laptop Imaginative and prescient (ICCV), IEEE, 2017, http://dx.doi.org/10.1109/iccv.2017.324. Accessed 15 Could 2023.
“Scatter Plot with Quadratic Polynomial Regression Curve.” Plotly, https://chart-studio.plotly.com/~aayushmittalaayush/14/#/. Accessed 15 Could 2023.
Staff, Keras. Keras Documentation: Losses. https://keras.io/api/losses/. Accessed 15 Could 2023.
Zhao, Xiaonan, et al. “A Weakly Supervised Adaptive Triplet Loss for Deep Metric Studying.” 2019 IEEE/CVF Worldwide Convention on Laptop Imaginative and prescient Workshop (ICCVW), IEEE, 2019, http://dx.doi.org/10.1109/iccvw.2019.00393. Accessed 15 Could 2023.